绪论

人工智能基本概念

1.自然界四大奥秘：物质的本质、宇宙的起源、生命的本质、智能的发生；

2.智能的定义：智能是只是和智力的总和；

3.智能的特征：

感知能力（游戏AI必须品）：主动信息的输入，实现视觉、听觉、触觉、嗅觉等感觉器官；
记忆力和思维能力：信息的存储和信息的模拟，记忆存储由感知器官感知到的外部信息以及由思维所产生的知识，思维能力对记忆的信息进行处理；
- 逻辑思维（抽象思维）：例如理科生通过逻辑去肢解一道数学题；
- 形象思维（直感思维）：例如人的第五感；
- 顿悟思维（灵感思维）：例如牛顿如何发现了力学；
学习能力：被动信息的输入，学习既可能是自觉的、有意识的，也可能是不自觉的、无意识的；既可以是有教师指导的，也可以是通过自己实践的；
行为能力（表达能力）：信息的输入，人工智能实现的目的；

人工智能发展简史

人工智能发展史：了解就好了，知乎看看就好；
人工智能发展史 - 知乎 (zhihu.com)

人工智能研究的基本内容

1.知识表达：将人类知识形式化或者模型化，方法有符号表示法、连接机制表示法，简单点说就是建立一个能把人懂的东西弄成机器能懂的东西的东西；

2.机器感知：使机器（计算机）具有类似于人的感知能力。以机器视觉(machine vision)与机器听觉为主；

3.机器思维：对通过感知得来的外部信息及机器内部的各种工作信息进行有目的的处理；

4.机器学习：研究如何使计算机具有类似于人的学习能力，使它能通过学习自动地获取知识；

5.机器行为：计算机的表达能力，即“说”、“写”、“画”等能力；

人工智能的主要研究领域

主要领域：自动定理证明、博弈、模式识别、机器视觉、自然语言理解、机器翻译、智能信息检索、数据挖掘与知识发现、专家系统、自动程序设计、机器人、组合优化问题、人工神经网络；

其他领域：分布式人工智能与多智能体、智能控制、智能仿真、智能CAD 、智能CAI 、智能管理与智能决策、智能多媒体系统、智能操作系统、智能计算机系统、智能通信、智能网络系统、人工生命；

知识表示与知识图谱

知识和知识表示

知识的概念

1.知识的定义：把有关信息关联在一起所形成的信息结构；

2.知识的作用：反映了客观世界中事物之间的关系；

3.知识的特性：

相对正确性：知识在一定的条件及环境下产生的才是正确的；
不确定性：
- 随机性引起的不确定性：清明一般都会下雨，但是也有不下雨的时候；
- 模糊性引起的不确定性：根据人的外貌去判断年龄；
- 经验引起的不确定性：经历丰富的人相对知识也更加丰富；
- 不完全性引起的不确定性：比如对人类对宇宙的了解并不完整；
可表示性和可利用性：知识可以用适当形式表示和利用；

知识表示的概念

1.知识表示的定义：将人类的知识形式化或者模型化（人类划重点）；

2.知识表示的作用：计算机可以接受的描述知识的数据结构

3.知识选择方法的原则：有利于知识的充分表示和分利用、便于组织、维护、管理、理解和实现；

一阶谓词逻辑表示法

非专业作了解：
人工智能一阶谓词逻辑表示法

产生式表示法

非专业作了解：
产生式表示法

框架表示法

非专业作了解：
知识表示之框架表示法

知识图谱（推荐学习）

定义：是一种揭示实体之间关系的语义网络；
目的：知识图谱的目的是为了提高搜索引擎的能力，改善用户的搜索质量以及搜索体验；

1.知识图谱的逻辑结构：

数据层：主要是由一系列的事实组成，而知识以事实为单位进行存储。
模式层：构建在数据层之上，是知识图谱的核心。

2.知识图谱的原始数据类型：

结构化数据：是指知识定义和表示都比较完备的数据，如关系数据库；
半结构化数据：是指部分数据是结构化的，但存在大量结构化程度较低的数据，如XML、JSON；
非结构化数据：是指没有定义和规范约束的“自由”数据，如文本、视频、音频、图片；

了解更多：
通俗易懂解释知识图谱

确定性推导方法

非专业作了解：
确定性推理方法

不确定性推导方法

非专业作了解：
不确定推理方法

搜索求解策略

搜索的概念

1.搜索算法主要解决问题：

是否一定能找到一个解。
找到的解是否是最佳解。
时间与空间复杂性如何。
是否终止运行或是否会陷入一个死循环

2.搜索方向：

从初始给出的条件出发；
从目的地出发，进行逆推算；
（A*算法）从开始状态出发作正向搜索，同时又从目的状态出发作逆向搜索，直到两条路径在中间的某处汇合为止；
状态空间的搜索策略
非专业作了解：
状态空间表示法

盲目的图搜索策略

回溯策略

1.回溯策略的数据结构：

Pass集合：记录寻路算法中的可走路径，保存搜索路径的状态，如果找到了目的，该集合就是解；
Open集合：等待搜索或者待访问的状态集合；
Close集合：已经被访问的状态集合；

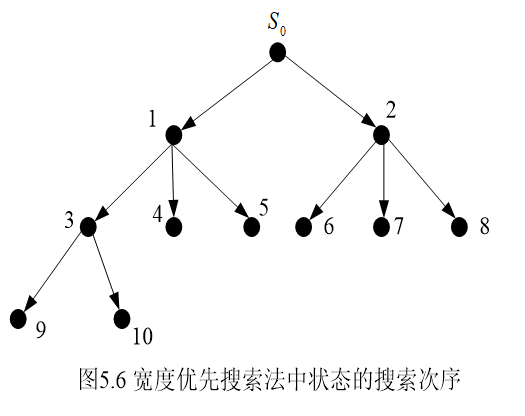
广度优先搜索策略

1.算法特点：如下俩点

每次选择深度最浅的节点首先扩展，搜索是逐层进行的，如图5.6所示；
一种高价搜索，会遍历所有节点，但若有解存在，则必能找到它，且是最短路径（可以理解很多人沿着不同的方向走，人多力量大）；

2.算法描述如下：

a：选择一个未访问的顶点入队；
b：从队里选出一个顶点V出队，并且标记为已经访问；
c：将顶点V的所有未被访问的邻接顶点入队并且设置该节点父节点为顶点V；
d：重复步骤a~b，直到所有顶点都已经被访问；
e：反向输出父节点，就是要找的路径（当然可能有多条，但是只返回一条）

3.核心算法实现：

/// <summary>
/// 广度优先算法BFS
/// </summary>
/// <param name="originNode">起点位置</param>
/// <param name="targetNode">目标位置</param>
/// <param name="passNodeList">可走路径</param>
public static void BFSSearch(Node originNode, Node targetNode, ref List<Node> passNodeList)
{
    Queue<Node> openQue = new Queue<Node>();
    openQue.Enqueue(originNode);

    while (openQue.Count > 0)
    {
        Node head = openQue.Dequeue();
        //获取该节点周围的节点
        List<Node> neighborLst = Program.GetNeighbor(head);

        //检查周围的节点
        for (int i = 0; i < neighborLst.Count; i++)
        {
            Node neighborNode = neighborLst[i];
            //节点被访问或者是障碍物的直接继续
            if (neighborNode.isVisit || neighborNode.nodeType == NodeType.Block) continue;
            //记录节点被访问
            neighborNode.isVisit = true;
            //记录父节点
            neighborNode.parent = head;
            openQue.Enqueue(neighborNode);

            //这个时候整个地图已经遍历完了
            if (neighborNode.Equals(targetNode))
            {
                //反向输出父节点，就是要找的路径
                while (!neighborNode.Equals(originNode))
                {
                    neighborNode = neighborNode.parent;
                    passNodeList.Add(neighborNode);
                    neighborNode.nodeType = NodeType.Pass;
                }
                //最后添加目标点（其实直接返回目标节点也是可以的）
                passNodeList.Add(targetNode);
                targetNode.nodeType = NodeType.Pass;
                return;
            }
        }
    }
}

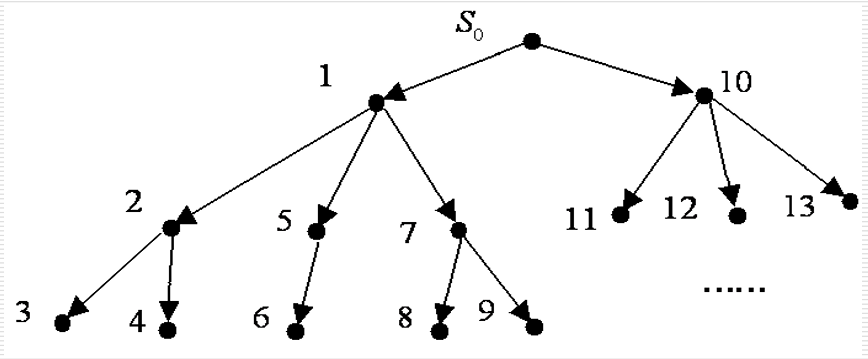
深度优先搜索策略

1.算法特点：

扩展最深的节点的结果使得搜索沿着状态空间某条单一的路径从起始节点向下进行下去；仅当搜索到达一个没有后裔的状态时，才考虑另一条替代的路径；
为了保证找到解，应选择合适的深度限制值，或采取不断加大深度限制值的办法，反复搜索，直到找到解；
深度优先搜索并不能保证第一次搜索到的某个状态时的路径是到这个状态的最短路径，如果路径距离很重要的话，它应该尝试保留最短路径；

深度优先算法搜索次序